もう接頭辞が苦しくなってきた「約数見つけてみるヤツ」です。4回目。
・「3の倍数を見つける方法」
・「続・3の倍数を見つける方法」
・「新・3の倍数を見つける方法」
とやってきましたが、剰余使えばもっと早く桁を小さくできるやん…
と思いついたので、説明しまーす。
目次
「あまり」を使うと…
基本的には今までの内容をちょっと拡張したいだけなので、新しいことは言わないです。
で、「あまり」。剰余ですな。
あまりの計算は整数を扱うときはめちゃくちゃ重要なんですよね。
んで、今回は
\[ある自然数nである自然数aを割った時のあまりをr_a、\\nである自然数bを割った時のあまりをr_bとしたとき、\\「(a+b)÷nのあまりは(r_a+r_b)になる」。\]
という性質を使ってやろうという魂胆。
この性質、合同式の性質で出てきますね。(俺は整数論やってないので、さっき知りました←)
性質使ってみる。
まぁつまりは、
\[n桁の整数N,任意の整数xについて、\\Nを10^k進法で\left\lceil\frac{n}{k}\right\rceil桁の整数と考えられるとき、\\m桁目に\frac{(x-l)^{m-1}}{(\frac{x}{10^k})^{n-m}}を掛け、\\その各桁の数の総和がlの倍数なら、Nはlの倍数\]
という演算をやった時、3行目で出せる多項式で総和を取る前に、
「各項を\(x\)で割って剰余をそれぞれ出し、その剰余の総和を取った時、『多項式の総和』と『剰余の総和』同士が法\(x\)で合同なんだから、『剰余の総和』の方使えば「判定するための値」の桁数減らせるやん!」
ということです。
前回、具体的な数字で試してたので、それを使って説明します!
こんな感じ。
「123456789」という整数は「9で割れんの?」って話だったんですが、
とりあえず、「1,23,45,67,89」と区切って、\(k=2\)としてやれば…
\[100-9=91\]
なので、各桁に\(91^{m-1}\)を掛けて多項式を作ると、
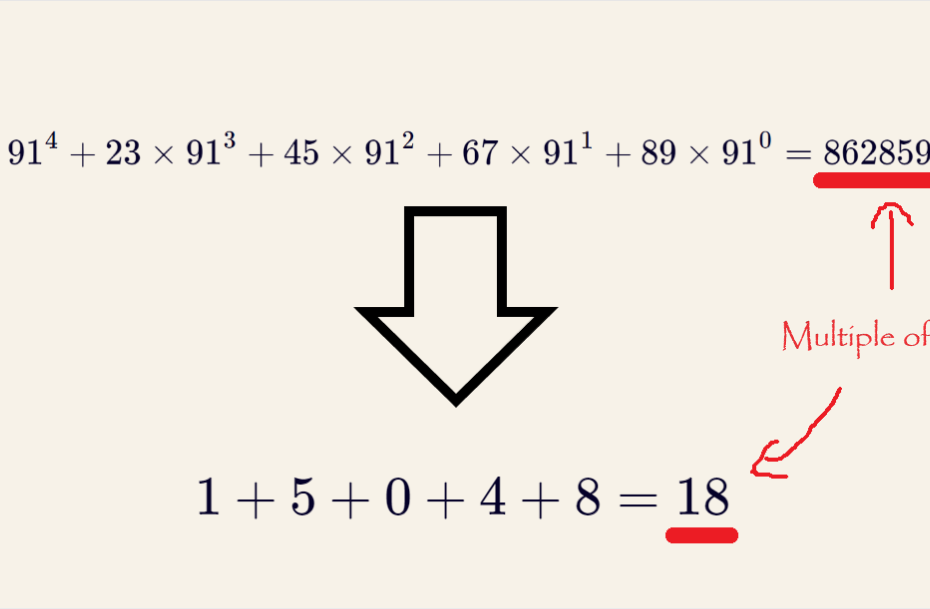
\[1×91^4+23×91^3+45×91^2+67×91^1+89×91^0=86285925\]
…まで出したのが前回の話。今回は、
\[1×91^4+23×91^3+45×91^2+67×91^1+89×91^0 \]
の各項を9で割って剰余を出して足す、という作業。
作業量は増えるけど、数字が小さいうちに作業できる点がメリット。
たぶんメモリの空間が狭くても行けんじゃね?的な。計算はしないよ!
では計算開始。
ここらへんも、合同式の性質をうまく使ってやると楽なんですよね。
ここで、プログラミング言語でよく見る「二項演算子”%”をつかった剰余演算」の表記法を借りてやると(「あまり」を一発で出せる演算、として使ってやると)、
$$91\%9=1$$
ということが正直パッと見で分かります。
そして合同式の性質から、
\[(91^2)\%9=1^2=1\\(91^3)\%9=1^3=1\\(91^n)\%9=1^n=1\]
という、超絶ラクチンな数字が出てくることが分かりました。
もう\(91^n\)の所はガン無視できそうです。
ということで、
\[1×91^4+23×91^3+45×91^2+67×91^1+89×91^0 \]
が
\[1+5+0+4+8=18\]
となり、18は9で割り切れるので、「123456789」は9で割り切れるということが分かりましたよ。
劇的に桁数が減ったよ!
単純に総和取るパターンでもそうですが、「9で割り切れる(かどうか)」以外の情報は切り捨ててしまっているので、
「18は2も約数である」ことは意味がないことに注意です。
「86285925は5も約数である」ことも意味がないです。よろしく。
とりあえず、判定が簡単になりました。
(簡単になるとは言っていない)
まぁ、資源が少なくても判定できそうじゃね?と思っての追記です。
アルゴリズムがこんな感じなのを組んで、超絶デカい整数を素因数分解できたりするんかな…とかいう夢を見ました。白昼夢です。
今回はそんな感じ!
整数って奥が深いね…
これで、中学受験で謎のデカい整数(デカい素数とデカい素数2つの積)を割らせる問題が出ても大丈夫だぞ!
という感じで〆ます。またこのあたりで思いついたら書きます。
ばーい👋
関連記事

更新情報をプッシュ通知
させることが出来ます。
よろしければm(__)m