3の倍数を見つける方法

3の倍数

問題。

「4972741564513716」という数字。

これは3の倍数でしょうか？

答え。これは3の倍数です。

どうやって判別したかって？

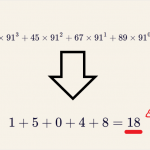
「4+9+7+2+7+4+1+5+6+4+5+1+3+7+1+6 = 72」で、これが3の倍数だから。

ホントかどうか割ってみると…

4972741564513716÷3 = 1657580521504572

うん、割り切れた。

これは、

「各桁を足して3の倍数になればその数字は3の倍数」

という技なんです。

有名なんで、結構聞いたことある方も多くいらっしゃるかと思います。

同じようなものに「9の倍数」判定ってのもあって、

「各桁を足して9の倍数になればその数字は9の倍数」

と。同じですな。
試しにさっきの数字の足した数が9の倍数(72)ということで割ってみましょう。

4972741564513716÷9 = 552526840501524

うん、整数。

あ、ちなみに

「『各桁を足して3の倍数になれば』『その数字は3の倍数』」
は
「『各桁を足した数字が3で割り切れたら』『その数字は3を約数として持つ』」
でも同じ意味です。『』の最初同士、最後同士を入れ換えても可。

他にもあった、全部足す技

こうなると、ほかの数字でもできないかなーって思いますよね。

検索すると…

どうやら11の倍数の判定が似てますねぇ。その内容とは、

「各桁を順番に『足して、次の桁は引いて、その次は足して…』と計算して、11の倍数になればその数字は11の倍数」

と。ちょっと面倒くさくなってますが。

ところで、最近暇を持て余していたので、この問題をずっと考えてました。

ほんと暇人ですねぇ～

それで、7の倍数もちょっとだけイジると、同じようになる方法を考えつきました。

「右から○桁目に3^○-1を掛けて各桁を足したとき、7の倍数になればその数字は7の倍数」

というもの。ええ、指数です。何乗とかいうやつです。

とりあえず指数といえば…

「3⁴ = 3×3×3×3」
☝(本体の数字) を (右肩の小さい数字) の分だけ掛け算するって意味
「3⁰ = 1」
☝0乗は1。3じゃなくてもすべての数字が1になります。πでも0でも。

これらを踏まえておいてください。

7の倍数

では気を取り直して、ホントかどうか検証してみましょう。

「14」って7の倍数ですよね？じゃあこれをさっきの説明通りに、

「1×3^2-1 + 4×3^1-1」……ということは「1×3 + 4×1 = 7」

7の倍数だね！え？納得いかない？

じゃあ217とか。217 は 31×7なので7の倍数です。では、

「2×3^3-1 + 1×3^2-1 + 7×3^1-1」
……ということは「2×9 + 1×3 + 7×1 = 28」
7の倍数になりました。

正しそうな気もするが…？
証明しましょう。

7の倍数、証明

$$N:知りたい整数,n:Nの桁数,k:Nの桁目,a_{k}:Nのm桁目の数字$$

$$N,n,k,a_k∈N_0$$

とりあえず$N$を上で定義した数字たちを使って表現すると、
\[
N = \sum_{k=1}^n 10^{k-1} a_k
\]
って表すことができます。そして今回の肝である「処理したらまた7の倍数」ってのは
\[
\sum_{k=1}^n 3^{k-1} a_k =7M
\]
という式にできます。これらを駆使して、
\[N=7(何かしらの整数)\]
これ言えれば勝ち。ドン勝です。
さて、どうしましょうか。引いてみますか。
\[
N-7M=\sum_{k=1}^n (10^{k-1}-3^{k-1}) a_k
\]
ふむ。どうにかしたい項といえば…
\[
(10^{k-1}-3^{k-1})
\]
これですな。

…………。あっ！
\[
a^2-b^2=(a-b)(a+b)
\]
これ思い出した！2乗だけじゃなくて、ずっとこの(a-b)がうまく出てきてくれないかなぁ…
\begin{eqnarray*}
a^n-b^n&=&(a-b)\sum_{k=0}^{n-1}a^k b^{n-1-k}\\&=&(a-b)α_n\tiny{←Σの項がウザいのでαになってもらいました}
\end{eqnarray*}

いやぁ、でるんですなぁ！うまくできてますわぁ！

これをさっきの式に当てはめてやれば…
\[
10^{k-1}-3^{k-1}=(10-3) α_k
\]
これこれー！そしてー
\begin{eqnarray*}
N-7M&=&\sum_{k=0}^{n} [(10-3) α_k a_k]\\
&=&\sum_{k=0}^{n} 7 α_k a_k\\
&=&7\sum_{k=0}^{n}α_k a_k
\end{eqnarray*}
ｷﾀ━━━━(ﾟ∀ﾟ)━━━━!!
7出ました！
あとは移項して
\begin{eqnarray*}
N&=&7\sum_{k=0}^{n}α_k a_k+7M\\
&=&7[\sum_{k=0}^{n}α_k a_k +M]
\end{eqnarray*}

$N=7(何かしらの整数)$の形ですね。ドン勝です！

はて、これって。ほかの数字でも行けそうじゃないですか？