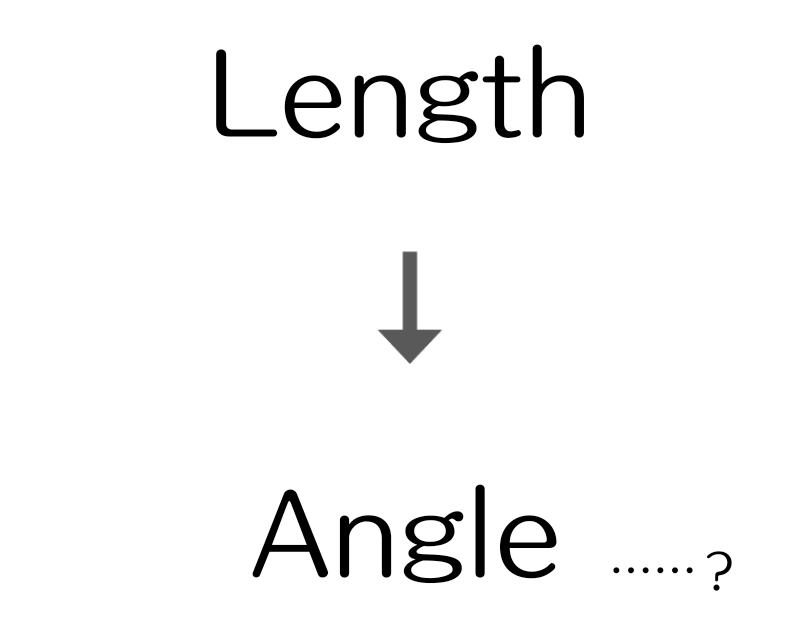
Q:「1m先の5m幅の棒」と「10m先の50m幅の棒」があります。
どっちが長く見えるでしょうか??
A:同じ長さに見える。
ですね。
「どんな計算だよ」って?
その前に、「自分の視線方向と直交する方向に延びる『長さ』」をどう認識してるかを見てみましょう。
目次
長さは角度で測ってる件
「長さ」を意識的にも無意識的にも、認識するときは「角度」に変換しています。たぶん。
…たぶん、ではあるんですが……
仮に上の文章が正しいとして、それを絵にしてみました。
絵にする
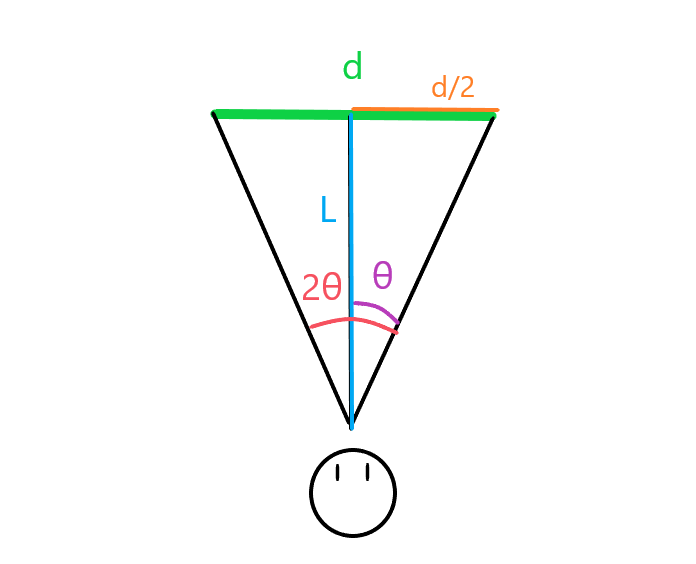
つまり絵の中の、
「『横幅:d(黄緑)』が『横方向の角度:2θ(赤)』に変換して認識している」
ということ。
これが正しそうな理由として、「遠近感」の存在があるということ。
冒頭に書いた「1m向こうの5m棒」と「10m向こうの50m棒」は、
それぞれどうあがいても「5m棒」と「50m棒」であることは絶対に変わらないですが、見た目は同じに見えます。
これが遠近感ですが、上の絵はその遠近感を正しく説明してるんじゃね?と。
「『俺から黄緑のやつまでの距離:L(水色)』長くしつつ、『黄緑のやつ:d(黄緑)』の長さは固定」だと、「2θ(赤)」はどんどん狭まっていくので、
「短くなっていくように見える!」という。
ほら、割とあってそう。
式立ててみる
とりあえず上の絵の「dから2θに変換する式」を立ててみましょう。
Lとdが直交してるモデルを想定しているので、直角三角形が出来ますよね。
そこでL、dからタンジェントを求められます。
$$\tanθ=\frac{d}{2L}$$
これで片側半分で「dとθの関係式」が出来ました。
次は「θ=」の式に。両辺をアークタンジェントで処理。
$$θ=\arctan\left(\frac{d}{2L}\right)$$
次は2θにしましょう。Lとdの交点はdの中点としているので、単純に2倍。
$$2θ=2\arctan\left(\frac{d}{2L}\right)$$
これ。dで2θが出せました。
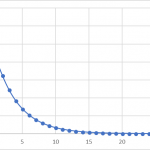
これを、d固定でLを変数とすると…
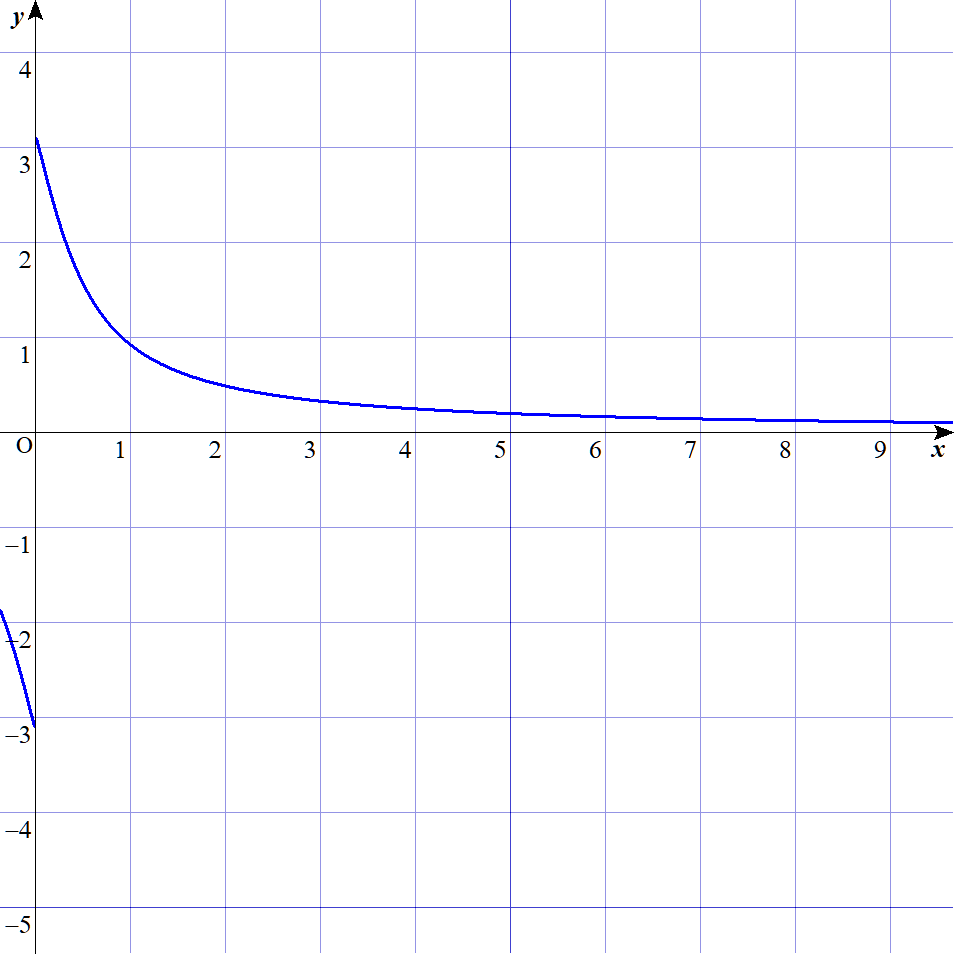
書いてる文字は気にするな!
あーどんどん小さくなってく!
(L>0)では単調減少ですね。
L=0の意味
でもさぁ、L=0って意味ある?
だって密着して棒を見てる状態だよ??
→なんで?危なくないよ
L=0の時に「1m先で5mに見えた棒が0m先(=密着)で∞mに見える」
という論調を
「0m先(=密着)ではどの長さも同じπ[rad](=180°)で見れる」
という論にするための式なので意味あります!
上は直感でも実際も間違ってるし。
下の論理はあってるし。
まぁ正解でしょう。ね!?
「2点間」は大抵「角度」
これは中学くらいまでには知っておきたい常識になるべきだと思ってます。
マジで。ホントにマジで!
この考えを持つだけで、「近いものAと遠いものAについて、遠いものAの方が小さく見える」が自明になりますし。
あと、極座標形式が瞬時に理解できます。これ重要。
イメージだけでいいので、ぜひこの考え方を持ってみることをお勧めします。
そんな感じ。ばーい👋
(追記するかも?)
関連記事

更新情報をプッシュ通知
させることが出来ます。
よろしければm(__)m