目次
大きい数への対応
もうちょっと語ります。
残る問題、大きい数の倍数を見つける方法。
「1桁」の最大値を増やしちゃえばいいんですよ。\(10\)進数のものなら\(10^n\)進数にしてしまいましょう。
具体的には、
「123456789」は9桁の整数、ですが
100進数と考えると、「”1″ “23” “45” “67” “89”」の”5″桁の整数と考えることができます。
これは隣の桁と重なっちゃうこともなく、すんなり考えられます。
ところで、そういう変換をしたときに、
$$n桁の整数N,任意の整数xについて、\\m桁目に\frac{(x-l)^{m-1}}{(\frac{x}{10})^{n-m}}を掛け、\\その各桁の数の総和がlの倍数なら、Nはlの倍数$$
の何を変えればいいでしょう?
なんか10ってあるなぁ。これを100に変えたら…?
つまり
$$n桁の整数N,任意の整数xについて、\\m桁目に\frac{(x-l)^{m-1}}{(\frac{x}{100})^{n-m}}を掛け、\\その各桁の数の総和がlの倍数なら、Nはlの倍数$$
とする、と。
…すこし説明が足りないですな。「1桁」の大きさの事も盛り込みましょうぜ。
$$n桁の整数N,任意の整数xについて、\\Nを10^2進法で\left\lceil\frac{n}{2}\right\rceil桁の整数と考えられるとき、\\m桁目に\frac{(x-l)^{m-1}}{(\frac{x}{10^2})^{n-m}}を掛け、\\その各桁の数の総和がlの倍数なら、Nはlの倍数$$
的な。
実際にやってみる
検証してみましょう。
せっかくなので「1,23,45,67,89」使いましょう。
9の倍数かどうかを検証してみると。
\[100-9=91\]
なので、各桁に\(91^{m-1}\)を掛けていきます。
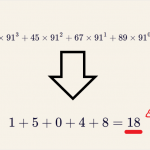
\[1×91^4+23×91^3+45×91^2+67×91^1+89×91^0=86285925\]
…ピンとこないなぁ。何回やっても9の倍数になるはずなので、わかりそうなところまでやってみましょ。
\[
\tiny{
\begin{eqnarray*}
86×91^3+28×91^2+59×91^1+25×91^0&=&65044368\\
65×91^3+4×91^2+43×91^1+68×91^0&=&49019220\\
49×91^3+1×91^2+92×91^1+20×91^0&=&36941652\\
36×91^3+94×91^2+16×91^1+52×91^0&=&27908478\\
27×91^3+90×91^2+84×91^1+78×91^0&=&21099429\\
21×91^3+9×91^2+94×91^1+29×91^0&=&15908103\\
15×91^3+90×91^2+81×91^1+3×91^0&=&12056229\\
12×91^3+5×91^2+62×91^1+29×91^0&=&9089928\\
9×91^3+8×91^2+99×91^1+28×91^0&=&6857424\\
6×91^3+85×91^2+74×91^1+24×91^0&=&5232069\\
5×91^3+23×91^2+20×91^1+69×91^0&=&3960207\\
3×91^3+96×91^2+2×91^1+7×91^0&=&3055878\\
3×91^3+5×91^2+58×91^1+78×91^0&=&2307474\\
2×91^3+30×91^2+74×91^1+74×91^0&=&1762380\\
1×91^3+76×91^2+23×91^1+80×91^0&=&1385100\\
1×91^3+38×91^2+51×91^1+0×91^0&=&1072890\\
1×91^3+7×91^2+28×91^1+90×91^0&=&814176\\
81×91^2+41×91^1+76×91^0&=&674568\\
67×91^2+45×91^1+68×91^0&=&558990\\
55×91^2+89×91^1+90×91^0&=&463644\\
46×91^2+36×91^1+44×91^0&=&384246\\
38×91^2+42×91^1+46×91^0&=&318546\\
31×91^2+85×91^1+46×91^0&=&264492\\
26×91^2+44×91^1+92×91^0&=&219402\\
21×91^2+94×91^1+2×91^0&=&182457\\
18×91^2+24×91^1+57×91^0&=&151299\\
…………
\end{eqnarray*}
}
\]
なげーよ!わかったよ!9の倍数だよ!
(※出来た数字は全て9で割れます。電卓叩いてみて!)
あと、ムダに数字の減り方をグラフにしました。ご査収ください。
まぁこういうグラフですよね。
一般化
一般化しましょうか。
$$n桁の整数N,任意の整数xについて、\\Nを10^k進法で\left\lceil\frac{n}{k}\right\rceil桁の整数と考えられるとき、\\m桁目に\frac{(x-l)^{m-1}}{(\frac{x}{10^k})^{n-m}}を掛け、\\その各桁の数の総和がlの倍数なら、Nはlの倍数$$
倍数知りたくなったら、最寄りの10の指数を訪ねるといいということでした!
ばーい
関連記事

更新情報をプッシュ通知
させることが出来ます。
よろしければm(__)m