あまりにも暇すぎてUnityでゲーム作ってみた件⑨(Directional Light の方向)

太陽の向き、って考えたことある？

地球にするということは、太陽もリアルにしたい！

Directional Lightの方向をシステムの時間で制御してやってリアルタイムに光の方向を変えてみましたよ。ムダに凝りだすやつ。

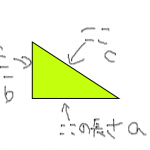
日時計の仕組み

まずは現在時刻の取得。

nowTimeに「0時00分00秒(UTC)から何分経ったか」を突っ込んでます。

なんで”分”かって？特に理由はないです。たまたま。

まずはnowTimeで太陽の向きを決めていきたいんだけど、まず、時刻と太陽の位置の関係から。

・正午に南中高度最大

・24時間周期( = 1440分周期)

・深夜0時に真裏に太陽

・y軸周りをぐるぐる回る

ということで、z-x平面上でDirectional Lightの方向ベクトルを回してやればいいわけです。

ベクトルを回すってことはy軸向きベクトルを軸にしてRotationか！ってなりそうですが、今回は違う方法を採ります。

っつーのも、時刻で方向決め打ち出来るから！っていうのと、このあとやろうとしてることも盛り込んだ結果こっちの方がよさげかなということで、方向のベクトルにぶち込むスタイルにしました。

Unityの「0」 -初期状態- を知る

よし、そうなればさっそくベクトルを入れるぞーとなるんですが、初期位置(Directional Lightのパラメータを全部0)でどういう向きになるかを見なくてはいけませんね。

どれどれ…

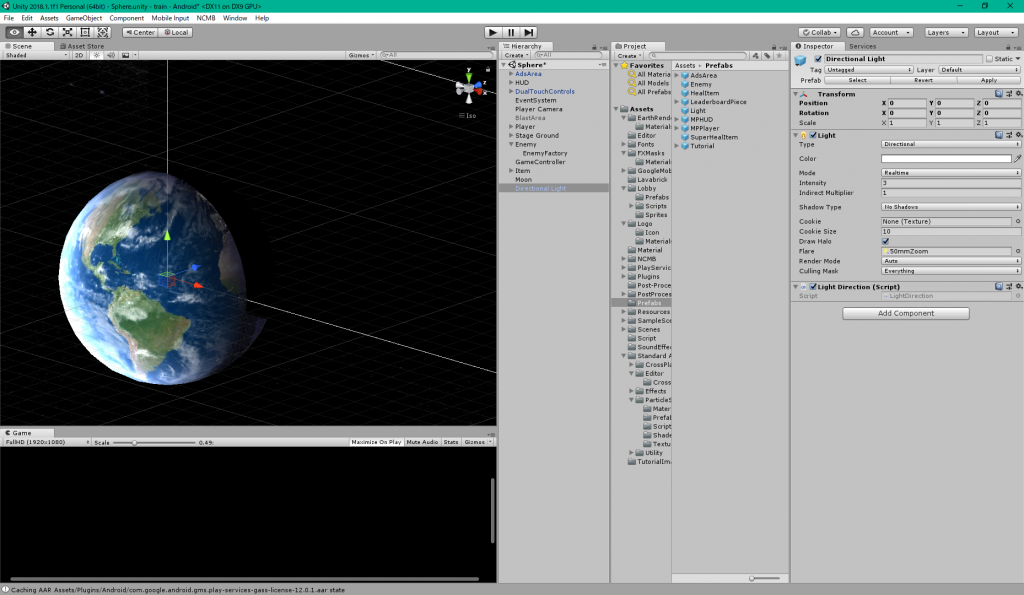
Directional Light の光の方向は青い矢印(forward)か…

さて問題。地球の経度の基準は？

そうですね本初子午線ですね。

さてどこでしょう？

そうですねグリニッジ天文台あたりですね。

ところでUTCという時刻は何基準でしょう？

そうですね本初子午線ですね。

つまり！ロンドンあたりの方向を0としたい！

画像だとわかりづらいですが、赤矢印が大体そっち向いてるんですな。

そうなると、0の時の光の方向正さないと！ってなるんですが。

日時計、答え合わせ

とりあえず結論は

nowDir.x = Mathf.Cos(nowTime * 2f * Mathf.PI / 1440f);

nowDir.z = Mathf.Sin(–nowTime * 2f * Mathf.PI / 1440f);

こうなりました。

見やすく数式にすると、
\[
\rm{nowDir.x} = cos(\frac{今の時間×2π}{1440})\\
\rm{nowDir.z} = sin(\frac{今の時間×2π}{1440})
\]

nowTime = 0なら

x = 1

z = 0

nowTime = 360(6時)なら

x = 0

z = -1

あってそう。

すげー三角関数出まくってます。覚えてる？え、知らない？気持ち悪くなってきたって？

何か回転するときは三角関数がほぼ絶対出てきますえ。

あと、回転させるなら、いつものx-y-z座標よりも極座標のほうが扱いやすいですえ。

とまぁ、これで完成ですな！

とはならず…

地球の自転軸は傾いているのでそれも考慮してみましょう。これがないと季節がなくなるぅ！

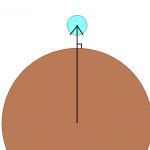
傾いてる球体

…ウィキペディアによると、地球の赤道傾斜角は23.44°(14.5.23時点)らしい。

この赤道傾斜角によって何が起きるかといえば、夏至冬至が発生するということですな。

というわけで今日の日付を取得して、計算だ！

nowDayはDayOfYearで1月1日から何日経ったかを取得してます。

ここは日で計算してるので多少ガバっても気にならないということで、

夏至冬至は本来年ごとに違う日になるのですが、今回は「1/1から173日後が夏至」と言い切ることにしました。ぱっと見じゃ気づかないからセーフ。

それらを考慮して式に当てはめると…

nowDir.x = Mathf.Cos(-(23.44f) / 180f * Mathf.PI * Mathf.Cos((nowDay – 173f) * 2f * Mathf.PI / 365f)) * Mathf.Cos(nowTime * 2f * Mathf.PI / 1440f)

nowDir.z = Mathf.Cos(-(23.44f) / 180f * Mathf.PI * Mathf.Cos((nowDay – 173f) * 2f * Mathf.PI / 365f)) * Mathf.Sin(-nowTime * 2f * Mathf.PI / 1440f)

これらも数式化すると、

\[
x = \cos\left(-\frac{23.44}{180}π×\cos\left(\frac{\left(今の日付-173\right)×2π}{365}\right)\right)×\cos\left(\frac{今の時間×2π}{1440}\right)\\
z = \cos\left(-\frac{23.44}{180}π×\cos\left(\frac{\left(今の日付-173\right)×2π}{365}\right)\right)×\sin\left(\frac{今の時間×2π}{1440}\right)
\]

おーけー！完璧だ！

ちょっと待ってください。傾いたということは、z-x平面からはみ出てますよね？ね？

満を持してy軸の登場でーす！

nowDir.y = Mathf.Sin(-(23.44f) / 180f * Mathf.PI * Mathf.Cos((nowDay – 173f) * 2f * Mathf.PI / 365f))

つまり

\[
y = \sin\left(-\frac{23.44}{180}π×\cos\left(\frac{\left(今の日付-173\right)×2π}{365}\right)\right)
\]

今度こそこれで完璧！

お疲れさまでした。

ところでnowDirの長さってずーっと1なんですよ。うるさくないベクトルなんですよ。

\[
\begin{eqnarray}
x&=& \cos\left(φ\right)×\cos\left(θ\right)\\
y&=& \sin\left(φ \right) \\
z&=& \cos\left(φ\right)×\sin\left(θ\right)\\
\end{eqnarray}\\
(θは地球をぐるぐるする角度、φは傾き補正のやつ角度としてます)\\
\]

\[
として、
\sqrt{x^2+y^2+z^2}を求めると…\\
\begin{eqnarray}
\sqrt{x^2+y^2+z^2} &=& \sqrt{\cos^2(φ)×\cos^2(θ)+\sin^2(φ)+\cos^2(φ)×\sin^2(θ) } \\
&=& \sqrt{\cos^2(φ)×(\cos^2(θ)+ \sin^2(θ) )+\sin^2(φ)} \\
\\
\cos^2θ+\sin^2θ=1なので、\\
\\
&=& \sqrt{\cos^2(φ)+\sin^2(φ)} \\
&=& \sqrt{1}\\
&=& 1\\
\end{eqnarray}
\]

ね！

極座標万歳！

→⑩へすすむ

←⑧へもどる

↩introへ