あまりにも暇すぎてUnityでゲーム作ってみた件⑤(&クォータニオンの話)

回るカメラ

④のつづき。

今度はカメラを回す操作。プレイヤーの周りをぐるぐるぐるぐる🌀🌀🌀

//camera rotationのところ。44行目～ね。
^{まずifの条件式にPauseGame.pausingとかGameController.playerAliveとか出てるけど、ポーズ中動かせないとか死んだら動かせないとかちょっとまだ脳内会議で出てない話題を先取っちゃってるので無視してね💖}
ゴホン、、、

とりあえず中身は48行目～なんだけど、

(カメラのTransform).RotateAroundの説明は

「カメラ位置のベクトルを『プレイヤーの位置から伸びる(第一引数:Vector3)』『法線ベクトル(の単位ベクトル)を軸として(第二引数:Vector3)』『inputAxisで指定した方向に(第三引数:float)』回転させる」ってやつよ。

ちなみにinputAxisはスティックor方向キーの水平方向の入力の値をそのまま掛けてます。

プラスに倒せばプラス、マイナスならマイナス。単純。

あ、そうそう。ついでに言っとくと開発は当然PCなんでゲームパッドとかキーボードの方向キーが使えるんだけど、

目指すところはクロスプラットフォームで、スマホも視野に入れてるということで、

Standard AssetsにあったCrossPlatformInputManager入れてます。これはまた後ほど。

下ってどっち？

そして、次の

「var axis = ～」

「var rot = ～」

がとてつもなく重要なのである。ちなみに制作中ここでハマりました。

何がどうハマったのかというと…

怖い話

事の顛末をお話しします。。。

カメラの向きってどうやるんだべか～

あ～単純にLookAtとかカメラ向きをforwardでプレイヤーの方むけりゃそっち向くべか～

…と思い、単純にいたって単純に、forward・LookAtにdirection_btw(④参照)のベクトルを突っ込みました。

「おーちゃんと向くね！回るね！いいよ～」

プレイヤーの操作スクリプト(⑥で解説するよ！)も組み、カメラの向いてる方向に動くのも確認していました。この時点では全くもって問題はありませんでした。

いえ、問題がないように見えていただけだったのです。

「さて、地面球体のサイドの部分に行ってみよう！」

移動している間、どうも違和感があります。

「あれ、回転させると変なネジれが…」

サイドに近づけば近づくほど、ネジレが強くなっていきます。

「おかしい…どういうことだ…」

サイドを超えて、南極の方までいくと、

「プレイヤーが上に見える…？」

今まで見下ろしていた視点だったのが、見上げる視点へと変わっていきます。

「うわぁ！時空が歪んでおる！！」

わたしはそこで気づいてしまいました。そう。forwardやLookAtで一つのベクトルだけ指定すると、「カメラの上方向」は不定だ、と。

そして、どうやら上方向を指定しないと、y軸の+方向が勝手に上方向となること。

プレイヤーの初期位置は地面球体のテッペンにしていたので、気付かなかったのです。

ひええええええええ！あー恐ろしい！

結局、下ってどっち？

長い前置きでしたが、つまり、「カメラの視線の向き」と「カメラの鉛直方向」を指定してあげないと、「画面の上」は常に(0,1,0)寄りとなってしまうわけです。

どうにかその2方向を指定できないかなーと思い、

①「forwardと『right』 or 『up』を指定する(ネジレを指定できればいいので鉛直方向じゃなくても大丈夫だろう)」→失敗(最後に指定したベクトル以外の直交方向がデフォルトに戻っちゃう)

②「LookAtは向くオブジェクトだけじゃなく、カメラの上向きベクトルも同時に指定できるらしい」→成功

初めから言え！マジで！

まぁ、今回のようなカメラワークは特殊ではあるので、向くオブジェクトだけ引数に入れる説明しか検索で引っかからないってのはしょうがない。

分かったところでやってみる。

上のコードでは第二引数にrotって突っ込んでるけど、何？って話なので、順を追って説明。

説明しよう！

ベクトルの回転とクォータニオン

とりあえず重要人物たちの紹介を。

・var axis→ベクトル

・var rot→クォータニオンで回転させたベクトル

え、まって、クォータニオンってなによ？

…下で説明するのでとりあえず進むよ！

axis = Vector3.Cross(normVect, direction);

これは何がしたいのかというと、法線ベクトル(normVect)とカメラ向きのベクトル(direction)両方に直角になるベクトルを求めているのです。

そうCrossとはクロス積(外積)。

a×bとか書くやつ。え？知らない？…ウィキペディア見てきて！これは説明しないよ！

https://ja.wikipedia.org/wiki/%E3%82%AF%E3%83%AD%E3%82%B9%E7%A9%8D

とにかく、Vector3.Crossをつかうと、引数に指定した2つのベクトル両方と直角になるベクトルが取得できるわけですな。

んで、これで求めたベクトルはカメラで見て真横になるベクトルになります。そして地面の接ベクトルでもありますな。

なぜこれを求めたかというと、真横向きベクトルを軸にカメラをちょっと下向きへと回転したかったのです。

ちょっとだけ、前に

さて次。Quaternion.AngleAxisなんだけど、第一引数は回転角度、第二引数は軸です。

今回の回転角度は

Mathf.Acos(Vector3.Dot(direction.normalized, (target.position – camposition).normalized)) * 180 / Mathf.PI

分かりやすくするために省くとこ省いたり補足したりすると、

Acos(direction.normalized・(プレイヤーから見たカメラの位置のベクトル).normalized) * 180/π

日本語で書くと、

「(カメラの向きベクトルの単位ベクトル)と{(プレイヤーから見たカメラの位置のベクトル)の単位ベクトル}の内積のアークコサインを取って弧度法から度数法に変換」したよ！

って意味なんだけど…

単位ベクトル同士の内積の意味は、「それぞれのベクトルのなす角を知りたい」ってことです。

しかし、内積をとっても角度が出るわけじゃなく、cosθが出るだけなんですな(④参照)。

このcosθからθだけ取り出したいとき…そんな便利なのあるわけ…

逆にするもの

あるんですこれが！cosの逆関数と呼ばれる関数、

Acos(アークコサイン)さん！

書き方としてはほかに

arccos、acos、Cos^-1、(cos^-1)(←これは指数かも?)とか(頭文字を大文字にする意味は色々流派があるらしい…)

指数っぽいけど違うよ！…

この逆関数の性質は、

$$\arccos(\cosθ)=θ$$

はいそういうことです。使っていきましょう。

あと、このAcos関数はラジアン(弧度法:π/3みたいなの)で返すので、AngleAxis用に度数法(60°とかのやつ)に変えましょう。

角度が求められたらあとはさっき求めたベクトルを軸にこの角度分法線ベクトルを回転させましょう！ということで、51行目。

クイッと前倒しになったベクトルrot。

これをカメラの上方向に指定してLookAtミー！

長い。とりあえずこれで終わり。次いくぞー！

※以下クォータニオンの説明

～クォータニオンとは？(複素数を添えて)～

ハミルトンが見つけた複素数を拡張した数のことである！

日本語では四元数っていうんだけど…これを説明する前に…

まず複素数の説明。これが分からないと四元数もｲﾐﾌ

えーまず、「それ同士を掛け合わせると(-1)になる数」→「それ×それ=-1」

それ = “虚数単位 i”

をつかって、(aとbを実数とすると)

$$a+bi$$

で表す数の事、と。このaを実部(Real part)、bを虚部(Imaginary part)つって。

覚えてる？え？知らない？

この複素数ってベクトルみたいな振る舞いしたりするんだけど、まず、実部は実部としか、虚部は虚部としか足し引き出来ないって性質。

ベクトルの要素は同じとこしか足し引き出来ないって性質に似てるなぁ。

あとは複素数の絶対値って概念。あ、そもそも絶対値ってその数の符号(マイナス)を消した数。

これをもうちょっと広い意味にとらえて、原点(グラフとか数直線の0のとこ)からの距離って意味としても通りそうだね。

んで、複素数の絶対値ってのを原点からの距離ととらえるよ、ってのを覚えといて…

ある複素数「\(a+bi\)」の絶対値の2乗は…

\[
\begin{eqnarray}
|(a+bi)|^2 &=&(a+bi)×(a-bi)\\
&=&(a×a-a×bi+bi×a-bi×bi)\\
&=&{a×a-b×b×(i×i)}\\
&=&a×a + b×b
\end{eqnarray}
\]

ってなるよ、と。
ってことは…

$$|(a+bi)|=\sqrt{a×a + b×b}$$

うーん…これって？

ここでピタゴラスの定理ってのを思い出して！覚えてる？

下の絵を見てください。

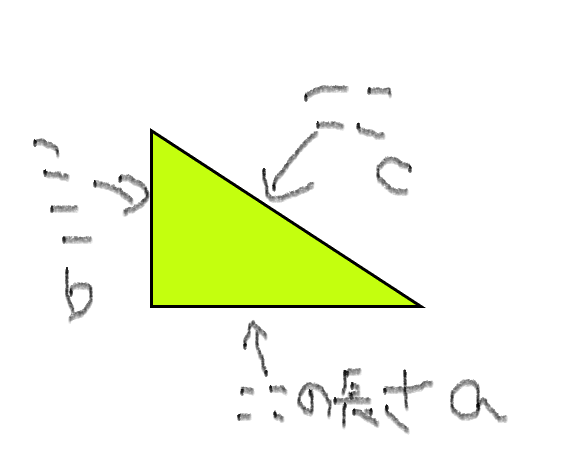
この三角形のcの長さをaとbを使って表すと～

$$c =\sqrt{a^2+b^2}$$

なんですね～…あれ、さっきのに似てる…

そんで、ベクトルの長さってx軸方向の長さとy軸方向の長さでピタゴラっちゃうんですが、(←めんどくさくなった)

それと似てるわけですよ。
複素数とベクトル、似すぎなんですよ(雑)

ただ、複素数はいわゆる「平面でのベクトル」に似てるだけで、Unity3Dで使うような三次元のベクトルとは似てないんですが…そこで！

ハミルトンさんが見つけた四元数！

複素数の虚数単位みたいなのが三つあって、

「虚数単位(四元数)i、j、k」ってのをつかって、(a,b,c,dを実数とすると)

$$四元数 = a+bi+cj+dk$$

と表せますよーと。
例によってaを実部、bcdを虚部ね。

…と思いきや、どうやら複素数が平面ベクトルっぽいってので味を占めたらしく、

実部を「スカラー部」、虚部を「ベクトル部」

って言うんだって！へー！

肝心の重要な性質が、複素数の「i²=-1」にあたる四元数の虚数単位の性質として

$$i^2=j^2=k^2=ijk=-1$$

$$ij=-ji=k$$

$$jk=-kj=i$$

$$ki=-ik=j$$

※地味に積は交換則満たさないので、かける順番が重要だよ！

…っていう数だよ～と。

んでこの四元数の性質で何が重要か。というか何が有用か。

回転が楽！なのである！

ベクトルの回転だとエグい量の計算を求められたりするけど、四元数だと掛けるだけ～らくらく～

そんなわけで四元数ことクォータニオンで回転させます。ベクトル。

→⑥へすすむ

←④へもどる

↩introへ