あまりにも暇すぎてUnityでゲーム作ってみた件④(&ベクトルの話)

やっとなんとなくオリジナルゲーム作りが始まります。

カメラを動かす。

ではまず操作。

操作なんですが、同時にカメラをどうにかしないといけません。

んでこういうスクリプトを書いてみました。Start()とUpdate()の抜粋ね。

カメラを動かす！ための準備

さて解説。

まずカメラ位置(//camera positionのとこ)だけど、

「まず29行目、地面にしてる球体の位置とプレイヤーの位置の差を取ってプレイヤーがいる位置での地面の法線ベクトルを作る(normVect)。そして次にプレイヤーの位置とカメラの位置の差でベクトル(direction_btw)を作っておく。これらをもとに、進行方向(まだ位置だけだから使わない)になる地面の接ベクトル(direction)を作るんだけど、考え方は『direction_btwからdirection_btwの法線方向成分を引いてあげる』ということで31行目見て。んで、カメラ位置はプレイヤーの位置から『法線方向に7、進行方向(現状向いてる方向)の逆方向に15』離れた位置にする、ってのが33行目。」

…( ﾟДﾟ)ﾊｧ?

絵で説明した方がよさそうだ。そんな高度な数学使ってないよ！たぶん高校くらいの数学しか使ってないよ！下手したら(ry

幾何学

えーつまり。

水色をプレイヤー、茶色を地面として…

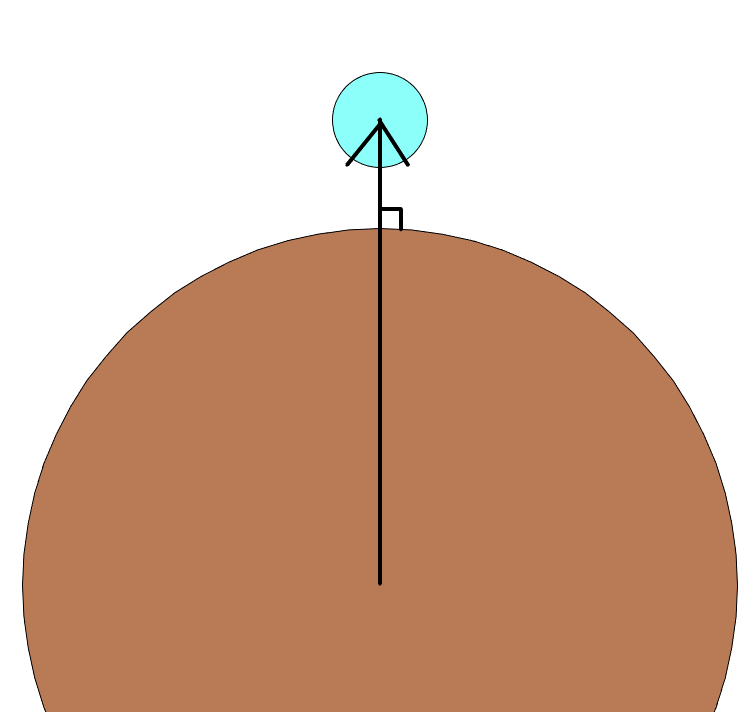
法線(直角って意味)ベクトル(normVect)はこう！☟

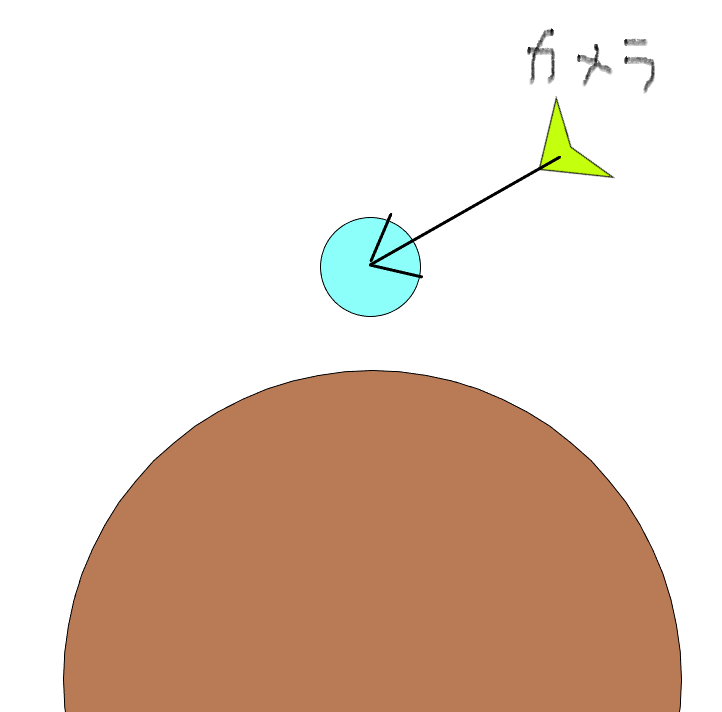
direction_btwはこう！☟

direction_btwをもとに接(そこに沿ってる、って意味)ベクトルを作ってるのはこう！☟

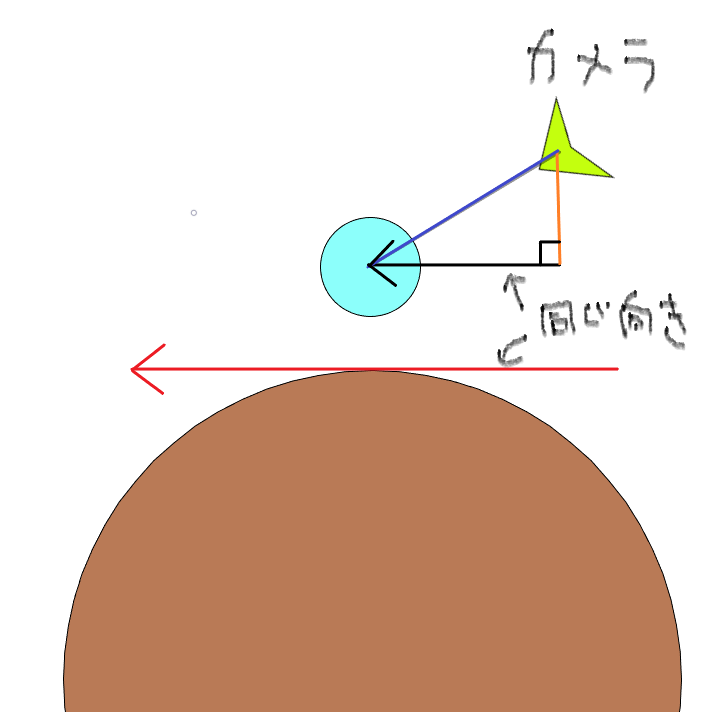
上の画像で、オレンジの線のベクトルを作るのに、normVect(の単位ベクトル)とdirection_btwとの内積をとってnormVectの単位ベクトルにかけてやる…と。

矢印の掛け算

あ、ここでちょっと脱線して、内積の話。

操作自体はそれぞれのベクトルの各成分同士を掛けて全部足すってだけなんですが、
そうすると、「同じ方向になる要素が掛け合わされる」みたいなことになるんですよね。

多分見たことあると思いますが、

$$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cosθ$$

的な式。
\(θ\)っつーのが\(\vec{a}\)と\(\vec{b}\)のなす角とかいう。\(|\vec{a}|\)とか\(|\vec{b}|\)は長さ。
長さだから向き関係なくなっちゃってるの。

あと、\(\vec{a}=(a,b,c)、\vec{b}=(x,y,z)\)とかいうベクトルだったとしたら、

$$\vec{a}\cdot\vec{b}=a×x+b×y+c×z$$

ね。覚えてる？え、知らない？まぁいいや。

ここで問題！\(\cosθ\)が1になるには？

そう！\(θ=0°\)になればいいんです！

つまり同じ方向向いたベクトルだと\(\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\)なので長さを掛けただけになるんですなぁ。

そして、\(\cosθ\)は0にもなるんですが、それは\(θ=90°\)のとき。

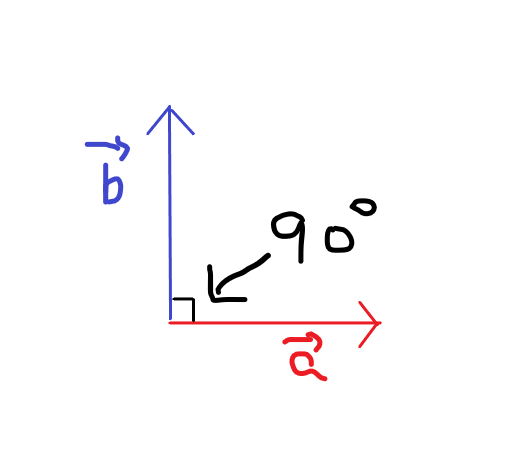
これこれこういうの。 \(\vec{a}\cdot\vec{b} =0\)になっちゃうんですなぁ。

φ(..)どれどれ…x軸向きの\(\vec{a}=(1,0,0)\)とy軸向きの\(\vec{b}=(0,1,0)\)だったら

$$\vec{a}\cdot\vec{b} = 1×0+0×1+0×0 = 0$$
あー0だわ。

内積の意味

これを総合すると、

「同じ向きのベクトルは残って、違う方を向いてる分は消える」

ということ。
これが言いたかった！

で。さっきの話に戻すと。

normVectとdirection_btwの内積をとると、direction_btwのnormVect方向の分だけが残るんですねぇ。

しかし問題が。
normVectの成分ってたぶん(800,0,200)とかなっちゃってると思うんですよ。
たぶんね！

そうすると、例えばdirection_btwが(765,961,876)とかいう成分だったら…

normVect・direction_btw\(=800×765+0×961+200×876\)

って感じで(最後まで計算しないけど)、ものすごくnormVectが主張してくるんですよ！
うるさすぎ！

normVectの役割はただ方向だけ教えてくれればよくて、お前の大きさなんか知ったこっちゃないんですよ。
邪魔なんですよそれ。

矢印を正規化

さて、うるさくない数字の代表格といえば……(ﾄﾞﾗﾑﾛｰﾙ)……

そう！＼ﾃﾞﾝ／

「1」！

単位元とかいうやつ。かけてもかけても同じ数字になるやつ。
ベクトルも「1」が一番うるさくないので、normVectも1にしましょう。

1にするにあたって。

\(\vec{a}\)の大きさは\(|\vec{a}|\)って話をしましたが、

これを使って\(\vec{a}\)の大きさを1にしてください。

単純に、同じ数字で割ると1になりますよね。

3÷3=1 とか、
100000000000000÷100000000000000=1 とか。

これ、ベクトルでもいけて、
\(\vec{a}\)を\(| \vec{a} |\)で割ります。 \(\vec{a}÷| \vec{a} |\) です。
これでうるさくない方向だけ教えてくれるベクトルができます。

とんちみたいだけど、これであってます。マジで。

…とまぁ、それはそうなんですが、
Unityさんにはうるさくないベクトルを作ってくれる機能があります。
「normalized」です。正規化。

さすがUnityさん痒い所に手が届く！

なお、このように作った「長さが1のベクトル」のことを
「単位ベクトル」
って言います。
さっき地味に出てて「？？？」になったなら、ここで覚えてってちょ！

役者はそろった…？

というわけでnormVect.normalizedでだした単位ベクトルと
direction_btwで内積をとって、法線ベクトル方向の成分を抜き出しましょう！

よしじゃあ法線ベクトル成分出たから引くぞ！

あ！

どうやって！

内積の結果はベクトルじゃないんですなぁ。
スカラーとかいうんだけど、つまりただの数字で方向もクソもないわけです。
じゃあどうすんのよ…

向き的には法線ベクトルの向きを思い浮かべてやってきたのに向きのない数字に変わりやがって…

向き…向き…そういえばさっき向きだけのうるさくないベクトルつくったよね？

法線ベクトルの。
で、欲しいのは法線ベクトルと同じ向きの大きさがdirection_btwの法線ベクトル成分のやつ。

掛けましょう。さあ。

役者、呼んできました

normVect.normalized × (抜き出した法線ベクトル成分)
☝これが欲しかったベクトル！

この作ったベクトルをもとのdirection_btwから引いちゃいましょう。
ベクトル同士は普通に足し引きできるので引いてください。

すると…

direction_btwの法線ベクトル成分が0のベクトルの出来上がり！

やった！

はぁはぁ…疲れたね…休憩…

数学嫌いになりそう…

おい！このスクリプトの半分も説明できてない気がするぞ！おい！

続きは次で。

→⑤へすすむ

←③へもどる

↩introへ