音名を認識するときのはなし

音名を認識するときってどんな感じですかね？

っていう雑記です。

適当に読んでってちょ。

音名とは？

音名はいわゆる「ド」とか「ソ」とかいうやつなんですが…

…なんて書くとややこしくなりそうですね。
今回「音名」と呼ぶのは、「相対音名=階名」のこととして話を進めます。
絶対音名じゃないですよ。

そもそも絶対音名・相対音名ってなによ？
ということで、

言葉をなんとなく定義

・絶対音名
ある振動数(×\(2^n\))の音に唯一結び付けられる名前のこと

・相対音名
“基準とする”ある振動数(×\(2^n\))の音を「ド」 としたときに、
そのドとの音程により付けられる名前(ドも含む)のこと

みたいなところでしょうか。

絶対音感を持ってる方は、ハ長調のハ音(C音)を「ド」と呼ぶことが多いかなと。
C=ドとすれば、上の絶対音名と相対音名が一致するので、そのように考えてもらってもかまいません。

言葉を定義するときにさらっと
「ある振動数(×\(2^n\))の音に」
と書きましたが、今回の注目ポイントはここです！

音名ってループするよね

「ド」の1オクターブ上の音はなんと呼ぶか。
→「ド」

じゃあ「ファ♯」の2オクターブ下の音はなんと呼ぶか。
→「ファ♯」

じゃあじゃあ「シ♭」の50000オクターブ上の音はなんと呼ぶか。
→絶対聴こえないけど「シ♭」

オクターブの関係こそが、
「ある振動数(×\(2^n\))の音…」
のはなしなんです。

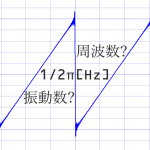
振動数が2倍=1オクターブ上
振動数が4倍=2オクターブ上
振動数が8倍=3オクターブ上

という感じ。これを踏まえつつ。

いったん、平均律のはなし

ピアノの鍵盤って、1オクターブの間に何個あるでしょうか。
12個あるんですね～
ド～シで12個。

12音にしたのは平均律が出来る以前の話ですが、
その平均律以前では半音間毎に振動数比率が異なっていて、移調・転調が難しかったそうな。
じゃあ間を等間隔にしてやれ！ってのが平均律。

この1オクターブ間を12等分すると、
「半音間の比率が\(2^{\frac{1}{12}}=\sqrt[12]{2}\)倍」
になります。

これも踏まえといてください。

ループしても音名を認識する=円状？

ここが本題ですわ。
五度圏みたいに、12音を等間隔に円周上に置いてやれ！ってなりました。
なぜなら13個目を等間隔で置いたとき、1個目と同じ場所に置かれるから。
1音目と13音目は同じ音名で呼ばれることに似てません？

そんなのもあって、どうせなら振動数を数字のまま使えるようにしてやれと思い、考え付いたのがこの式。

音名\(X=e^{2πi \log_2 \frac{ν_θ}{ν_0}}\)

但し、\(e\):自然対数の底、\(π\):円周率、\(i\):虚数単位、
\(ν_θ\):音名\(X\)となる音の振動数、\(ν_0\):基準音の振動数

みたいな。
これ、平均律だけじゃなくて、純正律とかピタゴラス音律とか、音律に関係なく使えるかなと。
平均律がきれいに並べられるようになるのは、半音の比率が全部同じってだけなので、この式の定義とは実は関係ないという。
定義するときはオクターブの関係しか使ってないんですよね。実は。

多分我々はこういう風に音名をとらえているはずです。

とか仰々しく言ってみる。

倍音がどういう音に聴こえるか

純正律って、1次元のモードで出てくるいわゆる整数倍の倍音から作られてるんですよね。
純正律と平均律がどのくらい近くてどのくらい遠いのかを、さっきの式で視覚化すると…

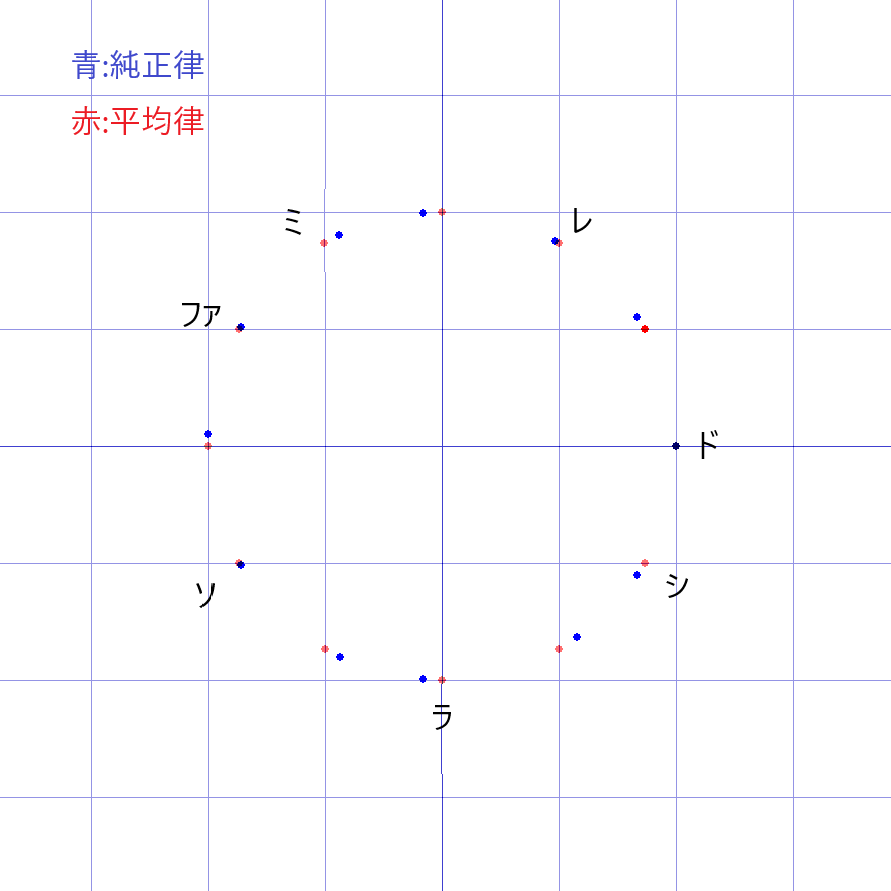
「ド」は同じ位置です。
こうやってみると「ファ」と「ソ」以外結構違う音なんですな…
俺的には「ラ」が全然違うのが衝撃…

さてさて、ある振動数の音に混ざりうる倍音のうち、基音(「ある振動数」×1の音)を「ド」としたとき、2倍、3倍、…
としていくと、どんな音になるんじゃ！？
ということで…

結構「あいだの微分音」が多いですね…
そして、これを683までやると「基準をドとした時」の「ファ」になると。

「純正律のファ」は一生出ないのでよろしくです。
「平均律のファ」に近いものを追い求めると、683くらい。
無限に数字を大きくすればもっと近いのがでるかも？
聴こえないけどね！

なお、「純正律のソ」は3ででてます。
「純正律のミ」は5、「平均律のミ」っぽいのは645あたりの模様。

音楽はやっぱり数学っぽいね

大した数学は使ってないですが、やはり定量的に扱える物理現象由来の
「感覚」
によって
「音感」
が引き起こされるので、親和性は非常に高いですね。

ということで、
「音名の認識が円っぽい」からの「数式化」でした。
「〇♪」。

ばーい👋